
그래프

특징
1.노드(vertax)와 간선(edge)으로 구성
2.간선 방향을 가지는 방향 그래프와 방향이 없는 무향 그래프로 나눈다
3.순환구조를 가진다
4.간선에 같은 가중치를 줄 수도 있고, 다르게 줄수도 있다.
(거리를 계산할 때, 가중치를 줄 수 있다)
방향그래프와 무방향 그래프

무방향은 10개
방향은 20개
공간복잡도
공간이 얼마나 있는지
공간이 얼마나 필요한지 계산하는 것
인접행렬

노드끼리 연결되었다면 1
그렇지 않다면 0
공간복잡도 - O(V^2)
(O는 최악으로 봤을때 겨우를 생각하는 것
O는 big o notation
아무것도 없을 때)
인접 리스트 방식
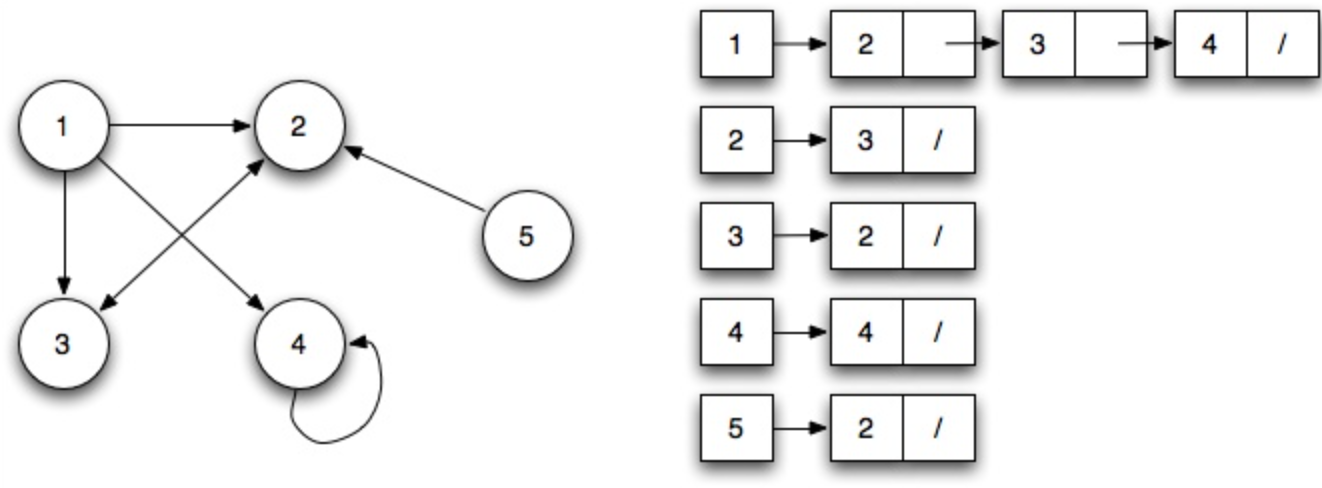
공간복잡도 - O(V+E)
정점 + 간선이라서 v+e
각 배열 방에 있는 해당 노드와 인접한 노드들을 linked list로 나열해서 저장하는 방식
효율적인 것은 시간이 적게 드는 방식
인접행렬이 빈번할 때, 추가/삭제가 효율적이다
인접리스트가 추가/ 삭제가 효율적이다
Tree
루트 정점이 존재한다.(=최상위가 존재한다)
트리는 그래프의 한 종류이다
하나의 부모 노드만 가질 수 있다
이진탐색 트리는 최대 2개까지 자식 노드를 가질 수 있다
그냥 트리는 자식노드 갯수가 상관없다
리프는 자식이 없는 노드
리프의 깊이
방향 :루트, 왼쪽, 오른쪽

루트에 따라 전위, 중위, 후위로 나눔
전위순회 :루트 왼쪽 오른쪽 A- B- D- G- H- E- C- F
중위순회 :왼쪽 루트 오른쪽 G -H -D -E -B -F -C- A
후위순회 :왼쪽 오른쪽 루트
이진 트리
정 이진 트리
노드가 0개 혹은 2개를 가지고 있는 것
완전 이진 트리

나머지 레벨을 제외한 노드가 채워져 있는 것
왼쪽으부터 채워져 있는 것이다
포화 이진 트리

노드가 2개씩 달려있는 것
완벽한 대칭
이진 탐색 트리
1. 자식 노드를 최대 2개까지 가질 수 있다
2. 항상 왼쪽 서브트리에는 작은 값, 오른쪽에는 큰 값이 존재
3. 원하는 값을 찾기 위해서는 최대 트리의 높이(h)가 필요하다
이진탐색트리를 정렬하여 출력하기 위한 순회 방법은 '중위순회' 이다

전위순회
트리를 복제하고 싶을때 쓴다.
후위순회
삭제할 떄는 가장 가까운 값을 찾아서 바꿔준다.

왼쪽은 가장 큰값
오른쪽은 가장 작은값
보통 오른쪽 서브트리에서 가장 작은값을 가져온다
근데, 왼쪽으로 해도 상관없다
이진탐색트리에서 시간 복잡도
추가 O(N)
삭제 O(N)
조회 O(N)
원래는 O(logN)이 맞다 -밸런스의 경우
근데, 최악의 경우를 생각해서 O(N) - 한쪽으로 치우친 경우
너비우선탐색은 스텍, 큐
'프로그래밍 기본 용어' 카테고리의 다른 글
| 자료구조) 시간복잡도 (0) | 2020.12.08 |
|---|---|
| 자료구조) (0) | 2020.12.07 |
| 자료구조)Stack과 Queue (0) | 2020.12.03 |
| NPM 오류 제거, 모듈 확인 등 (0) | 2020.12.02 |
| 깃허브 (0) | 2020.12.01 |